Результат 1 из 1
Вопрос:
Вопрос с множественным выбором
А1. Среди чисел -7; 7⁻¹; 1/7;  ; -0,7 выберите число, противоположное числу 7.
; -0,7 выберите число, противоположное числу 7.
1) -7; 2) 7⁻¹; 3) 1/7; 4) 5) -0,7.
5) -0,7.
Результат 2 из 2
Вопрос:
Вопрос с множественным выбором
А2. Пусть О и О₁ − центры оснований цилиндра, изображённого на рисунке. Тогда образующей цилиндра является отрезок:
 1) OO₁; 2) LO; 3) MN; 4) LM; 5) LN.
1) OO₁; 2) LO; 3) MN; 4) LM; 5) LN.
Результат 2 из 2
Вопрос:
Вопрос с множественным выбором
А3. Среди точек А(0; -3); В(3; 0); С(-9; 3); О(0; 0); М(- ;
; ) выберите ту, которая принадлежит графику функции, изображённому на рисунке:
) выберите ту, которая принадлежит графику функции, изображённому на рисунке:
1) А; 2) В; 3) С; 4) О; 5) М.

Результат 2 из 2
Вопрос:
Вопрос с множественным выбором
А4. Найдите значение выражения
1) 2,2; 2) -1,4; 3) 0,2; 4) 1,4; 5) -0,2.
Результат 2 из 2
Вопрос:
Вопрос с множественным выбором
А5. Одно число меньше другого на 72, что составляет 18 % большего числа. Найдите меньшее число.
1) 328; 2) 390; 3) 900; 4) 480; 5) 472.
Результат 2 из 2
Вопрос:
Вопрос с множественным выбором
А6. На рисунке изображены развёрнутый угол АОМ и лучи ОВ и ОС. Известно, что ∟АОС = 102⁰, ∟ВОМ = 128⁰. Найдите величину угла ВОС.
1) 78⁰; 2) 50⁰; 3) 26⁰; 4) 52⁰; 5) 38⁰.
Результат 2 из 2
Вопрос:
Вопрос с множественным выбором
А7. Образующая конуса равна 34 и наклонена к плоскости основания под углом 60⁰. Найдите площадь боковой поверхности конуса.
1) 578 π; 2) 289π; 3) 289
π; 2) 289π; 3) 289 π; 4) 578π; 5) 1156π.
π; 4) 578π; 5) 1156π.
Результат 2 из 2
Вопрос:
Вопрос с множественным выбором
А8. Расположите числа 3,66; ; 3,(6) в порядке возрастания.
; 3,(6) в порядке возрастания.
1) ; 3,(6); 3,66; 2) 3,66;
; 3,(6); 3,66; 2) 3,66; ; 3,(6); 3) 3,(6);
; 3,(6); 3) 3,(6); ; 3,66; 4) 3,66; 3,(6);
; 3,66; 4) 3,66; 3,(6); ; 5)
; 5) ; 3,66; 3,(6).
; 3,66; 3,(6).
Результат 3 из 3
Вопрос:
Вопрос с множественным выбором
А9. Одна из сторон прямоугольника на 6 см длиннее другой, а его площадь равна 112 см². Уравнение, одним из корней которого является длина меньшей стороны прямоугольника, имеет вид:
1) x² + 112x - 6 = 0; 2) x² + 6x - 112 = 0; 3) x² - 112x + 6 = 0; 4) x² - 6x + 112 = 0; 5) x² - 6x - 112 = 0.
Результат 3 из 3
Вопрос:
Вопрос с множественным выбором
А10. Точки А(-1; 2) и В(2; 7) − вершины квадрата ABCD. Периметр квадрата равен:
Результат 3 из 3
Вопрос:
Вопрос с множественным выбором
А11. Упростите выражение

Результат 3 из 3
Вопрос:
Вопрос с множественным выбором
А12. Решением неравенства

Результат 3 из 3
Вопрос:
Вопрос с множественным выбором
А13. Найдите длину средней линии прямоугольной трапеции с острым углом 60⁰, у которой большая боковая сторона и большее основание равны 16.
Результат 3 из 3
Вопрос:
Вопрос с множественным выбором
А14. Упростить выражение

Результат 3 из 3
Вопрос:
Вопрос с множественным выбором
А15. Найдите сумму целых решений неравенства 5(x - 4) > (x - 4)².
1) 39; 2) 5; 3) 26; 4) -26; 5) -5.
Результат 4 из 4
Вопрос:
Вопрос с множественным выбором
А16. ABCDA₁B₁C₁D₁ − прямоугольный параллелепипед такой, что АВ = 20, AD = 4. Через середины рёбер АА₁ и ВВ₁ проведена плоскость (см. рисунок), составляющая угол 60⁰ с плоскостью основания ABCD. Найдите площадь сечения параллелепипеда этой плоскостью.
Результат 4 из 4
Вопрос:
Вопрос с множественным выбором
А17. Сумма наибольшего и наименьшего значений функции y = (3sin3x + 3cos3x)² равна:
1) 9; 2) 18; 3) 36; 4) 3; 5) 12.
Результат 4 из 4
Вопрос:
Вопрос с множественным выбором
А18. Корень уравнения (или их сумма, если корней несколько) принадлежит промежутку:
1) [-1; 0); 2) (0; 1); 3) [1; 2); 4) [2; 3); 5) [3; 4).

Результат 3 из 3
Вопрос:
Вопрос с множественным выбором
B1. Автомобиль проехал некоторое расстояние, израсходовав 12 л топлива. Расход топлива при этом составил 8 л на 100 км пробега. Затем автомобиль существенно увеличил скорость, в результате чего расход топлива вырос до 10 л на 100 км пробега. Сколько литров топлива понадобится автомобилю, чтобы проехать такое же расстояние?
Результат 3 из 3
Вопрос:
Вопрос с множественным выбором
B2. Решите уравнение

В ответ запишите сумму его корней (корень, если он один).
Результат 4 из 4
Вопрос:
Вопрос с множественным выбором
B3. Основание остроугольного равнобедренного треугольника равно 4, а синус противолежащего угла равен 0,8. Найдите площадь треугольника.
Результат 4 из 4
Вопрос:
Вопрос с множественным выбором
B4. Пусть (x; y) − целочисленное решение системы уравнений Найдите сумму х + у.

Результат 4 из 4
Вопрос:
Вопрос с множественным выбором
B5. Найдите наибольшее целое решение неравенства

Результат 4 из 4
Вопрос:
Вопрос с множественным выбором
B6. Найдите количество корней уравнения 5sin2x + 3cos4x + 3 = 0 на промежутке [- π/4; 2π].
Результат 4 из 4
Вопрос:
Вопрос с множественным выбором
B7. Геометрическая прогрессия со знаменателем 4 содержит 10 членов. Сумма всех членов прогрессии равна 30. Найдите сумму всех членов прогрессии с чётными номерами.
Результат 4 из 4
Вопрос:
Вопрос с множественным выбором
B8. Найдите сумму корней уравнения |(x - 5)(x - 10)|·(|x - 2| + |x - 12| + |x - 7|) = 11(x - 5)(10 - x)
Результат 5 из 5
Вопрос:
Вопрос с множественным выбором
B9. Из города А в город В, расстояние между которыми 300 км, одновременно выезжают два автомобиля. Скорость первого автомобиля на 20 км/ч больше скорости второго, но он делает в пути остановку на 45 мин. Найдите наибольшее значение скорости (в км/ч) первого автомобиля, при движении с которой он прибудет в В не позже второго.
Результат 0 из 5
(пропущено)
Вопрос:
Вопрос с множественным выбором
B10. Из точка А проведены к окружности радиуса 10/3 касательная АВ (В − точка касания) и секущая АС, проходящая через центр окружности и пересекающая её в точках D и C. Найдите площадь S треугольника АВС, если длина секущей АС в 3 раза больше длины касательной. В ответ запишите 2S.
Результат 6 из 6
Вопрос:
Вопрос с множественным выбором
B11. Если cos(α + 24⁰) = 0 < α + 24⁰ < 90⁰, то значение выражения 30cos(α + 69⁰) равно …
0 < α + 24⁰ < 90⁰, то значение выражения 30cos(α + 69⁰) равно …
Результат 6 из 6
Вопрос:
Вопрос с множественным выбором
B12. Решите уравнение
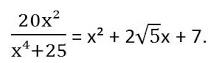
 bovaliservice
bovaliservice  +375 29 6226637
+375 29 6226637