Результат 1 из 1
Вопрос:
Вопрос с множественным выбором
А1. Укажите номер рисунка, на котором изображён равнобедренный треугольник:

Результат 2 из 2
Вопрос:
Вопрос с множественным выбором
А2. Укажите верное равенство:

Результат 2 из 2
Вопрос:
Вопрос с множественным выбором
А3. Сумма всех натуральных делителей числа 20 равна:
Результат 2 из 2
Вопрос:
Вопрос с множественным выбором
А4. Даны квадратные уравнения:
1) 3x² + 12x + 12 = 0; 2) 7x² - 3x - 2 = 0;
3) 5x² + 10x + 5 = 0; 4) 12x² + 4x + 5 = 0;
5) 2x² - 3x - 5 = 0.
Укажите уравнение, которое не имеет корней.
Результат 2 из 2
Вопрос:
Вопрос с множественным выбором
А5. Если 10²·α = 537,61278, то значение α с точностью до сотых равно:
1) 5,37; 2) 53,76; 3) 5,38; 4) 53761,28; 5) 5376,13.
| |
|---|
|
| 53761,28
|
|
| 5,37
|
|
| 5376,13
|
|
| 5,38
|
|
| 53,76
|
Ответ:
| 5,37
|
| 53761,28
|
| 5,38
|
| 53,76
|
| 5376,13
|
Результат 2 из 2
Вопрос:
Вопрос с множественным выбором
А6. Число 154 является членом арифметической прогрессии 4, 7, 10, 13, … . Укажите его номер.
Результат 2 из 2
Вопрос:
Вопрос с множественным выбором
А7. Решите неравенство |-x| ≥ 3.
| |
|---|
|
| x є [3; + ∞)
|
|
| x є (-∞; - 3]
|
|
| x₁ = - 3, x₂ = 3
|
|
| x є (-∞; - 3]U[3; + ∞)
|
|
| x є [- 3; 3]
|
Ответ:
| x є (-∞; - 3]
|
| x є (-∞; - 3]U[3; + ∞)
|
| x₁ = - 3, x₂ = 3
|
| x є [3; + ∞)
|
| x є [- 3; 3]
|
Результат 2 из 2
Вопрос:
Вопрос с множественным выбором
А8. Вычислите:

Результат 2 из 2
Вопрос:
Вопрос с множественным выбором
А9. Площадь круга равна 169π. Диаметр этого круга равен:
Результат 3 из 3
Вопрос:
Вопрос с множественным выбором
А10. Найдите наименьший положительный корень уравнения

Результат 3 из 3
Вопрос:
Вопрос с множественным выбором
А11. Четырёхугольник MNPK, в котором угол N = 136⁰, вписан в окружность.
Результат 3 из 3
Вопрос:
Вопрос с множественным выбором
А12. На одной чаше уравновешенных весов лежат 3 яблока и 1 груша, на другой – 2 яблока, 2 груши и гирька весом 20 г. Каков вес одной груши (в граммах), если все фрукты вместе весят 780 г? Считайте все яблоки одинаковыми по весу и все груши одинаковыми по весу.
Результат 3 из 3
Вопрос:
Вопрос с множественным выбором
А13. Прямая а, параллельная плоскости α, находится от неё на расстоянии 3. Через прямую а проведена плоскость β, пересекающая плоскость α по прямой b и образующая с ней угол 60⁰. Найдите площадь четырёхугольника ABCD, если A и B − такие точки прямой а, что AB = 2, а C и D − такие точки прямой b, что CD = 5.
Результат 3 из 3
Вопрос:
Вопрос с множественным выбором
А14. Упростите выражение
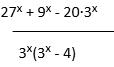
| |
|---|
|
| 2·3x
|
|
| 3x - 5
|
|
| 3x + 5
|
|
| 27x - 5
|
Ответ:
| 3x - 5
|
| 2·3x
|
| 27x - 5
|
| 3x + 5
|
Результат 3 из 3
Вопрос:
Вопрос с множественным выбором
А15. Корень уравнения


Результат 3 из 3
Вопрос:
Вопрос с множественным выбором
А16. Какая из прямых:
1) y = 3; 2) y = 4,8; 3) y = 0; 4) y = - 4; 5) y = - 2,7
пересекает график функции y = (1/2)x² + 2x + 5 в двух точках?
Результат 4 из 4
Вопрос:
Вопрос с множественным выбором
Результат 4 из 4
Вопрос:
Вопрос с множественным выбором
А18. Наименьшее целое решение неравенства lg(x² - 4x - 5) - lg(x + 1) ≤ lg3
равно:
Результат 3 из 3
Вопрос:
Вопрос с множественным выбором
В1. Если в правильной четырёхугольной пирамиде высота равна 3, а площадь диагонального сечения равна 9, то её объём равен …
Результат 3 из 3
Вопрос:
Вопрос с множественным выбором
В2. Найдите количество всех целых решений неравенства
(16x-x3) / (5x)>0
Результат 4 из 4
Вопрос:
Вопрос с множественным выбором
В3. Точки А(2; 2), B(7; 5) и C(8; 5) − вершины трапеции ABCD (AD||BC). Найдите сумму координат точки D, если BD =
Результат 4 из 4
Вопрос:
Вопрос с множественным выбором
В4. Найдите периметр правильного шестиугольника, меньшая диагональ которого равна 11
Результат 4 из 4
Вопрос:
Вопрос с множественным выбором
В5. Найдите произведение корней уравнения 3x² + 81 = 22-x²·6x²
Результат 4 из 4
Вопрос:
Вопрос с множественным выбором
В6. Площадь прямоугольника ABCD равна 55. Точки M, N, P, Q – середины его сторон. Найдите площадь четырёхугольника, заключённого между прямыми AN, BP, CQ, DM.
Результат 5 из 5
Вопрос:
Вопрос с множественным выбором
В7. Решите уравнение и найдите сумму его корней

Результат 5 из 5
Вопрос:
Вопрос с множественным выбором
В8. Найдите значение выражения 8cos(α + π/4), если sin2α = 23/32, 2α є (π/2; π)
Результат 5 из 5
Вопрос:
Вопрос с множественным выбором
В9. Найдите сумму целых значений x, принадлежащих области определения функции
y = logₓ₋₃(7 + 6x - x²)
Результат 5 из 5
Вопрос:
Вопрос с множественным выбором
В10. Прямоугольный треугольник с катетами, равными 1 и 2 , вращается вокруг оси, содержащей его гипотенузу. Найдите значение выражения 9V/π, где V − объём фигуры
, вращается вокруг оси, содержащей его гипотенузу. Найдите значение выражения 9V/π, где V − объём фигуры
Результат 6 из 6
Вопрос:
Вопрос с множественным выбором
В11. Из двух растворов с различным процентным содержанием спирта массой 200 г и 300 г отлили по одинаковому количеству раствора. Каждый из отлитых растворов долили в остаток другого раствора, после чего процентное содержание спирта в обоих растворах стало одинаковым. Найдите, сколько раствора (в граммах) было отлито из каждого раствора
Результат 6 из 6
Вопрос:
Вопрос с множественным выбором
В12. Найдите произведение корней уравнения x - =(x-5)/(2x+10)
=(x-5)/(2x+10)
 bovaliservice
bovaliservice  +375 29 6226637
+375 29 6226637