Результаты

Функция y = tgx не определена в точке:

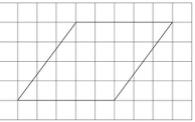
На клетчатой бумаге с клетками размером 1 см х 1 см изображён параллелограмм. Найдите его площадь в квадратных сантиметрах.

Если 15% некоторого числа равны 33, то 20% этого числа равны: 1) 44; 2) 46; 3) 55; 4) 56; 5) 66.

Если 9Х - 24 = 0, то 18Х - 31 равно:

Для любого числа х выражение 2³ˣ⁺⁴ - 2³ˣ равно:

От листа жести, имеющего форму квадрата, отрезали прямоугольную полосу шириной 7 дм, после чего площадь оставшейся части листа оказалась равной 30 дм². Длина стороны квадратного листа (в дециметрах) была равна:

Значение выражения 3⁻¹² ·(3⁻⁵)⁻² равно: 
 

Площадь осевого сечения цилиндра равна 10. Площадь его боковой поверхности равна:

Параллельно стороне треугольника, равной 5, проведена прямая. Длина отрезка этой прямой, заключённого между сторонами треугольника, равна 2. Найдите отношение площади полученной трапеции к площади исходного треугольника.

Сумма координат точки пересечения прямых, заданных уравнениями 2х+5у = 11 и х+у = 2(5-у), равна:

Количество целых решений неравенства

  на промежутке [-4; 5] равно:

Найдите наименьший положительный корень уравнения    4sin² x + 12cosx - 9 = 0.

Диагонали трапеции равны 15 и 20. Найдите площадь трапеции, если её средняя линия равна 12,5.

По двум перпендикулярным прямым, которые пересекаются в точке О, движутся две точки М₁ и М₂ по направлению к точке О со скоростями 1 м/с и 2 м/с соответственно. Достигнув точки О, они продолжают своё движение. В первоначальный момент времени М₁О = 5 м, М₂О = 20 м. Через сколько секунд расстояние между точками М₁ и М₂ будет минимальным?
 

Найдите 4x₁ · x₂ , где x₁ , x₂ − абсциссы точек пересечения параболы и горизонтальной прямой (см. рис.)

В арифметической прогрессии 130 членов, их сумма равна 130, а сумма членов с чётными номерами на 130 больше суммы членов с нечётными номерами. Найдите сотый член этой прогрессии.

В равнобокой трапеции большее основание вдвое больше каждой из остальных сторон и лежит в плоскости α. Боковая сторона образует с плоскостью α угол, синус которого равен  

. Найдите 36sinβ , где β − угол между диагональю трапеции и плоскостью α.

Основанием пирамиды SABCD является ромб со стороной и углом BAD, равным arccos(3/4). Ребро SD перпендикулярно основанию, а ребро SB образует с основанием угол 60⁰. Найдите радиус R сферы, проходящей через точки A, B, C и середину ребра SB. В ответ запишите R².